1180 lines
38 KiB
Rust
1180 lines
38 KiB
Rust
use std::cmp;
|
|
use std::fmt;
|
|
|
|
use crate::automaton::{AlwaysMatch, Automaton};
|
|
use crate::bytes;
|
|
use crate::error::Result;
|
|
use crate::stream::{IntoStreamer, Streamer};
|
|
|
|
pub use crate::raw::build::Builder;
|
|
pub use crate::raw::error::Error;
|
|
pub use crate::raw::node::{Node, Transitions};
|
|
|
|
mod build;
|
|
mod common_inputs;
|
|
mod counting_writer;
|
|
mod error;
|
|
mod node;
|
|
mod registry;
|
|
mod registry_minimal;
|
|
#[cfg(test)]
|
|
mod tests;
|
|
|
|
/// A sentinel value used to indicate an empty final state.
|
|
const EMPTY_ADDRESS: CompiledAddr = 0;
|
|
|
|
/// A sentinel value used to indicate an invalid state.
|
|
///
|
|
/// This is never the address of a node in a serialized transducer.
|
|
const NONE_ADDRESS: CompiledAddr = 1;
|
|
|
|
/// CompiledAddr is the type used to address nodes in a finite state
|
|
/// transducer.
|
|
///
|
|
/// It is most useful as a pointer to nodes. It can be used in the `Fst::node`
|
|
/// method to resolve the pointer.
|
|
pub type CompiledAddr = usize;
|
|
|
|
/// An acyclic deterministic finite state transducer.
|
|
///
|
|
/// # How does it work?
|
|
///
|
|
/// The short answer: it's just like a prefix trie, which compresses keys
|
|
/// based only on their prefixes, except that a automaton/transducer also
|
|
/// compresses suffixes.
|
|
///
|
|
/// The longer answer is that keys in an automaton are stored only in the
|
|
/// transitions from one state to another. A key can be acquired by tracing
|
|
/// a path from the root of the automaton to any match state. The inputs along
|
|
/// each transition are concatenated. Once a match state is reached, the
|
|
/// concatenation of inputs up until that point corresponds to a single key.
|
|
///
|
|
/// But why is it called a transducer instead of an automaton? A finite state
|
|
/// transducer is just like a finite state automaton, except that it has output
|
|
/// transitions in addition to input transitions. Namely, the value associated
|
|
/// with any particular key is determined by summing the outputs along every
|
|
/// input transition that leads to the key's corresponding match state.
|
|
///
|
|
/// This is best demonstrated with a couple images. First, let's ignore the
|
|
/// "transducer" aspect and focus on a plain automaton.
|
|
///
|
|
/// Consider that your keys are abbreviations of some of the months in the
|
|
/// Gregorian calendar:
|
|
///
|
|
/// ```plain
|
|
/// jan
|
|
/// feb
|
|
/// mar
|
|
/// may
|
|
/// jun
|
|
/// jul
|
|
/// ```
|
|
///
|
|
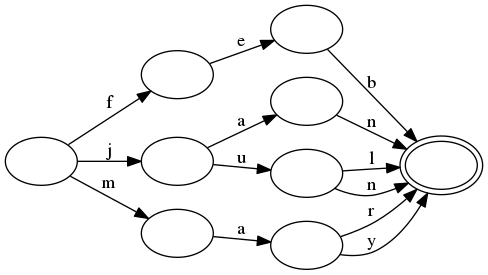
/// The corresponding automaton that stores all of these as keys looks like
|
|
/// this:
|
|
///
|
|
/// 
|
|
///
|
|
/// Notice here how the prefix and suffix of `jan` and `jun` are shared.
|
|
/// Similarly, the prefixes of `jun` and `jul` are shared and the prefixes
|
|
/// of `mar` and `may` are shared.
|
|
///
|
|
/// All of the keys from this automaton can be enumerated in lexicographic
|
|
/// order by following every transition from each node in lexicographic
|
|
/// order. Since it is acyclic, the procedure will terminate.
|
|
///
|
|
/// A key can be found by tracing it through the transitions in the automaton.
|
|
/// For example, the key `aug` is known not to be in the automaton by only
|
|
/// visiting the root state (because there is no `a` transition). For another
|
|
/// example, the key `jax` is known not to be in the set only after moving
|
|
/// through the transitions for `j` and `a`. Namely, after those transitions
|
|
/// are followed, there are no transitions for `x`.
|
|
///
|
|
/// Notice here that looking up a key is proportional the length of the key
|
|
/// itself. Namely, lookup time is not affected by the number of keys in the
|
|
/// automaton!
|
|
///
|
|
/// Additionally, notice that the automaton exploits the fact that many keys
|
|
/// share common prefixes and suffixes. For example, `jun` and `jul` are
|
|
/// represented with no more states than would be required to represent either
|
|
/// one on its own. Instead, the only change is a single extra transition. This
|
|
/// is a form of compression and is key to how the automatons produced by this
|
|
/// crate are so small.
|
|
///
|
|
/// Let's move on to finite state transducers. Consider the same set of keys
|
|
/// as above, but let's assign their numeric month values:
|
|
///
|
|
/// ```plain
|
|
/// jan,1
|
|
/// feb,2
|
|
/// mar,3
|
|
/// may,5
|
|
/// jun,6
|
|
/// jul,7
|
|
/// ```
|
|
///
|
|
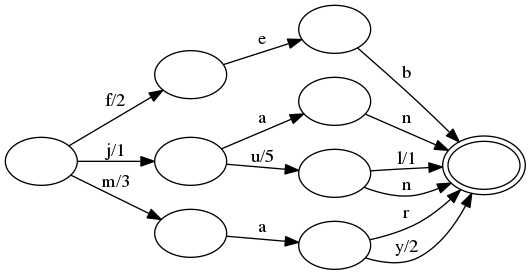
/// The corresponding transducer looks very similar to the automaton above,
|
|
/// except outputs have been added to some of the transitions:
|
|
///
|
|
/// 
|
|
///
|
|
/// All of the operations with a transducer are the same as described above
|
|
/// for automatons. Additionally, the same compression techniques are used:
|
|
/// common prefixes and suffixes in keys are exploited.
|
|
///
|
|
/// The key difference is that some transitions have been given an output.
|
|
/// As one follows input transitions, one must sum the outputs as they
|
|
/// are seen. (A transition with no output represents the additive identity,
|
|
/// or `0` in this case.) For example, when looking up `feb`, the transition
|
|
/// `f` has output `2`, the transition `e` has output `0`, and the transition
|
|
/// `b` also has output `0`. The sum of these is `2`, which is exactly the
|
|
/// value we associated with `feb`.
|
|
///
|
|
/// For another more interesting example, consider `jul`. The `j` transition
|
|
/// has output `1`, the `u` transition has output `5` and the `l` transition
|
|
/// has output `1`. Summing these together gets us `7`, which is again the
|
|
/// correct value associated with `jul`. Notice that if we instead looked up
|
|
/// the `jun` key, then the `n` transition would be followed instead of the
|
|
/// `l` transition, which has no output. Therefore, the `jun` key equals
|
|
/// `1+5+0=6`.
|
|
///
|
|
/// The trick to transducers is that there exists a unique path through the
|
|
/// transducer for every key, and its outputs are stored appropriately along
|
|
/// this path such that the correct value is returned when they are all summed
|
|
/// together. This process also enables the data that makes up each value to be
|
|
/// shared across many values in the transducer in exactly the same way that
|
|
/// keys are shared. This is yet another form of compression!
|
|
///
|
|
/// # Bonus: a billion strings
|
|
///
|
|
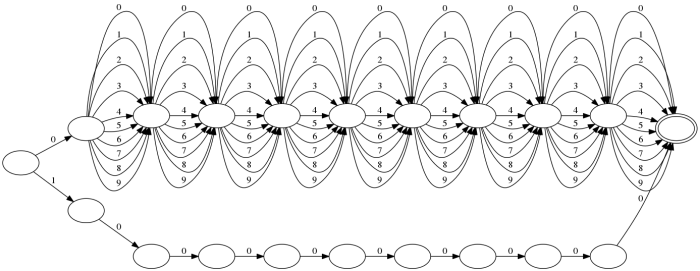
/// The amount of compression one can get from automata can be absolutely
|
|
/// ridiuclous. Consider the particular case of storing all billion strings
|
|
/// in the range `0000000001-1000000000`, e.g.,
|
|
///
|
|
/// ```plain
|
|
/// 0000000001
|
|
/// 0000000002
|
|
/// ...
|
|
/// 0000000100
|
|
/// 0000000101
|
|
/// ...
|
|
/// 0999999999
|
|
/// 1000000000
|
|
/// ```
|
|
///
|
|
/// The corresponding automaton looks like this:
|
|
///
|
|
/// 
|
|
///
|
|
/// Indeed, the on disk size of this automaton is a mere **251 bytes**.
|
|
///
|
|
/// Of course, this is a bit of a pathological best case, but it does serve
|
|
/// to show how good compression can be in the optimal case.
|
|
///
|
|
/// Also, check out the
|
|
/// [corresponding transducer](https://burntsushi.net/stuff/one-billion-map.svg)
|
|
/// that maps each string to its integer value. It's a bit bigger, but still
|
|
/// only takes up **896 bytes** of space on disk. This demonstrates that
|
|
/// output values are also compressible.
|
|
///
|
|
/// # Does this crate produce minimal transducers?
|
|
///
|
|
/// For any non-trivial sized set of keys, it is unlikely that this crate will
|
|
/// produce a minimal transducer. As far as this author knows, guaranteeing a
|
|
/// minimal transducer requires working memory proportional to the number of
|
|
/// states. This can be quite costly and is anathema to the main design goal of
|
|
/// this crate: provide the ability to work with gigantic sets of strings with
|
|
/// constant memory overhead.
|
|
///
|
|
/// Instead, construction of a finite state transducer uses a cache of
|
|
/// states. More frequently used states are cached and reused, which provides
|
|
/// reasonably good compression ratios. (No comprehensive benchmarks exist to
|
|
/// back up this claim.)
|
|
///
|
|
/// It is possible that this crate may expose a way to guarantee minimal
|
|
/// construction of transducers at the expense of exorbitant memory
|
|
/// requirements.
|
|
///
|
|
/// # Bibliography
|
|
///
|
|
/// I initially got the idea to use finite state tranducers to represent
|
|
/// ordered sets/maps from
|
|
/// [Michael
|
|
/// McCandless'](http://blog.mikemccandless.com/2010/12/using-finite-state-transducers-in.html)
|
|
/// work on incorporating transducers in Lucene.
|
|
///
|
|
/// However, my work would also not have been possible without the hard work
|
|
/// of many academics, especially
|
|
/// [Jan Daciuk](http://galaxy.eti.pg.gda.pl/katedry/kiw/pracownicy/Jan.Daciuk/personal/).
|
|
///
|
|
/// * [Incremental construction of minimal acyclic finite-state automata](https://www.mitpressjournals.org/doi/pdfplus/10.1162/089120100561601)
|
|
/// (Section 3 provides a decent overview of the algorithm used to construct
|
|
/// transducers in this crate, assuming all outputs are `0`.)
|
|
/// * [Direct Construction of Minimal Acyclic Subsequential Transducers](https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.24.3698&rep=rep1&type=pdf)
|
|
/// (The whole thing. The proof is dense but illuminating. The algorithm at
|
|
/// the end is the money shot, namely, it incorporates output values.)
|
|
/// * [Experiments with Automata Compression](https://www.researchgate.net/profile/Jiri-Dvorsky/publication/221568039_Word_Random_Access_Compression/links/0c96052c095630d5b3000000/Word-Random-Access-Compression.pdf#page=116), [Smaller Representation of Finite State Automata](https://www.cs.put.poznan.pl/dweiss/site/publications/download/fsacomp.pdf)
|
|
/// (various compression techniques for representing states/transitions)
|
|
/// * [Jan Daciuk's dissertation](http://www.pg.gda.pl/~jandac/thesis.ps.gz)
|
|
/// (excellent for in depth overview)
|
|
/// * [Comparison of Construction Algorithms for Minimal, Acyclic, Deterministic, Finite-State Automata from Sets of Strings](https://www.cs.mun.ca/~harold/Courses/Old/CS4750/Diary/q3p2qx4lv71m5vew.pdf)
|
|
/// (excellent for surface level overview)
|
|
#[derive(Clone)]
|
|
pub struct Fst<D> {
|
|
meta: Meta,
|
|
data: D,
|
|
}
|
|
|
|
#[derive(Debug, Clone)]
|
|
struct Meta {
|
|
root_addr: CompiledAddr,
|
|
len: usize,
|
|
}
|
|
|
|
impl Fst<Vec<u8>> {
|
|
/// Create a new FST from an iterator of lexicographically ordered byte
|
|
/// strings. Every key's value is set to `0`.
|
|
///
|
|
/// If the iterator does not yield values in lexicographic order, then an
|
|
/// error is returned.
|
|
///
|
|
/// Note that this is a convenience function to build an FST in memory.
|
|
/// To build an FST that streams to an arbitrary `io::Write`, use
|
|
/// `raw::Builder`.
|
|
pub fn from_iter_set<K, I>(iter: I) -> Result<Fst<Vec<u8>>>
|
|
where
|
|
K: AsRef<[u8]>,
|
|
I: IntoIterator<Item = K>,
|
|
{
|
|
let mut builder = Builder::memory();
|
|
for k in iter {
|
|
builder.add(k)?;
|
|
}
|
|
Ok(builder.into_fst())
|
|
}
|
|
|
|
/// Create a new FST from an iterator of lexicographically ordered byte
|
|
/// strings. The iterator should consist of tuples, where the first element
|
|
/// is the byte string and the second element is its corresponding value.
|
|
///
|
|
/// If the iterator does not yield unique keys in lexicographic order, then
|
|
/// an error is returned.
|
|
///
|
|
/// Note that this is a convenience function to build an FST in memory.
|
|
/// To build an FST that streams to an arbitrary `io::Write`, use
|
|
/// `raw::Builder`.
|
|
pub fn from_iter_map<K, I>(iter: I) -> Result<Fst<Vec<u8>>>
|
|
where
|
|
K: AsRef<[u8]>,
|
|
I: IntoIterator<Item = (K, u64)>,
|
|
{
|
|
let mut builder = Builder::memory();
|
|
for (k, v) in iter {
|
|
builder.insert(k, v)?;
|
|
}
|
|
Ok(builder.into_fst())
|
|
}
|
|
}
|
|
|
|
impl Fst<&'static [u8]> {
|
|
/// Creates a transducer from its representation as a raw byte sequence.
|
|
///
|
|
/// This operation is intentionally very cheap (no allocations and no
|
|
/// copies). In particular, no verification on the integrity of the
|
|
/// FST is performed. Callers may opt into integrity checks via the
|
|
/// [`Fst::verify`](struct.Fst.html#method.verify) method.
|
|
///
|
|
/// The fst must have been written with a compatible finite state
|
|
/// transducer builder (`Builder` qualifies). If the format is invalid or
|
|
/// if there is a mismatch between the API version of this library and the
|
|
/// fst, then an error is returned.
|
|
#[inline]
|
|
pub const fn new_unchecked(bytes: &'static [u8]) -> Fst<&'static [u8]> {
|
|
assert!(bytes.len() >= 16);
|
|
|
|
let end = bytes.len();
|
|
|
|
let root_addr = {
|
|
let i = end - 8;
|
|
|
|
u64_to_usize(u64::from_le_bytes([
|
|
bytes[i],
|
|
bytes[i + 1],
|
|
bytes[i + 2],
|
|
bytes[i + 3],
|
|
bytes[i + 4],
|
|
bytes[i + 5],
|
|
bytes[i + 6],
|
|
bytes[i + 7],
|
|
]))
|
|
};
|
|
|
|
let len = {
|
|
let i = end - 16;
|
|
|
|
u64_to_usize(u64::from_le_bytes([
|
|
bytes[i],
|
|
bytes[i + 1],
|
|
bytes[i + 2],
|
|
bytes[i + 3],
|
|
bytes[i + 4],
|
|
bytes[i + 5],
|
|
bytes[i + 6],
|
|
bytes[i + 7],
|
|
]))
|
|
};
|
|
|
|
let meta = Meta { root_addr, len };
|
|
|
|
assert!(
|
|
!((root_addr == EMPTY_ADDRESS && bytes.len() != 16)
|
|
&& root_addr + 21 != bytes.len())
|
|
);
|
|
|
|
Fst { meta, data: bytes }
|
|
}
|
|
}
|
|
|
|
impl<D: AsRef<[u8]>> Fst<D> {
|
|
/// Creates a transducer from its representation as a raw byte sequence.
|
|
///
|
|
/// This operation is intentionally very cheap (no allocations and no
|
|
/// copies). In particular, no verification on the integrity of the
|
|
/// FST is performed. Callers may opt into integrity checks via the
|
|
/// [`Fst::verify`](struct.Fst.html#method.verify) method.
|
|
///
|
|
/// The fst must have been written with a compatible finite state
|
|
/// transducer builder (`Builder` qualifies). If the format is invalid or
|
|
/// if there is a mismatch between the API version of this library and the
|
|
/// fst, then an error is returned.
|
|
#[inline]
|
|
pub fn new(data: D) -> Result<Fst<D>> {
|
|
let bytes = data.as_ref();
|
|
|
|
if bytes.len() < 16 {
|
|
return Err(Error::Format { size: bytes.len() }.into());
|
|
}
|
|
|
|
// The read_u64 unwraps below are OK because they can never fail.
|
|
// They can only fail when there is an IO error or if there is an
|
|
// unexpected EOF. However, we are reading from a byte slice (no
|
|
// IO errors possible) and we've confirmed the byte slice is at least
|
|
// N bytes (no unexpected EOF).
|
|
let end = bytes.len();
|
|
let root_addr = {
|
|
let last = &bytes[end - 8..];
|
|
u64_to_usize(bytes::read_u64_le(last))
|
|
};
|
|
let len = {
|
|
let last2 = &bytes[end - 16..];
|
|
u64_to_usize(bytes::read_u64_le(last2))
|
|
};
|
|
|
|
// The root node is always the last node written, so its address should
|
|
// be near the end. After the root node is written, we still have to
|
|
// write the root *address* and the number of keys in the FST, along
|
|
// with the checksum. That's 20 bytes. The extra byte used below (21
|
|
// and not 20) comes from the fact that the root address points to
|
|
// the last byte in the root node, rather than the byte immediately
|
|
// following the root node.
|
|
//
|
|
// If this check passes, it is still possible that the FST is invalid
|
|
// but probably unlikely. If this check reports a false positive, then
|
|
// the program will probably panic. In the worst case, the FST will
|
|
// operate but be subtly wrong. (This would require the bytes to be in
|
|
// a format expected by an FST, which is incredibly unlikely.)
|
|
//
|
|
// The special check for EMPTY_ADDRESS is needed since an empty FST
|
|
// has a root node that is empty and final, which means it has the
|
|
// special address `0`. In that case, the FST is the smallest it can
|
|
// be: the version, type, root address and number of nodes. That's
|
|
// 36 bytes (8 byte u64 each).
|
|
//
|
|
// And finally, our calculation changes somewhat based on version.
|
|
// If the FST version is less than 3, then it does not have a checksum.
|
|
let (empty_total, addr_offset) = (16, 21);
|
|
|
|
if (root_addr == EMPTY_ADDRESS && bytes.len() != empty_total)
|
|
&& root_addr + addr_offset != bytes.len()
|
|
{
|
|
return Err(Error::Format { size: bytes.len() }.into());
|
|
}
|
|
|
|
let meta = Meta { root_addr, len };
|
|
|
|
Ok(Fst { meta, data })
|
|
}
|
|
|
|
/// Retrieves the value associated with a key.
|
|
///
|
|
/// If the key does not exist, then `None` is returned.
|
|
#[inline]
|
|
pub fn get<B: AsRef<[u8]>>(&self, key: B) -> Option<Output> {
|
|
self.as_ref().get(key.as_ref())
|
|
}
|
|
|
|
/// Returns true if and only if the given key is in this FST.
|
|
#[inline]
|
|
pub fn contains_key<B: AsRef<[u8]>>(&self, key: B) -> bool {
|
|
self.as_ref().contains_key(key.as_ref())
|
|
}
|
|
|
|
/// Retrieves the key associated with the given value.
|
|
///
|
|
/// This is like `get_key_into`, but will return the key itself without
|
|
/// allowing the caller to reuse an allocation.
|
|
///
|
|
/// If the given value does not exist, then `None` is returned.
|
|
///
|
|
/// The values in this FST are not monotonically increasing when sorted
|
|
/// lexicographically by key, then this routine has unspecified behavior.
|
|
#[inline]
|
|
pub fn get_key(&self, value: u64) -> Option<Vec<u8>> {
|
|
let mut key = vec![];
|
|
|
|
if self.get_key_into(value, &mut key) {
|
|
Some(key)
|
|
} else {
|
|
None
|
|
}
|
|
}
|
|
|
|
/// Retrieves the key associated with the given value.
|
|
///
|
|
/// If the given value does not exist, then `false` is returned. In this
|
|
/// case, the contents of `key` are unspecified.
|
|
///
|
|
/// The given buffer is not clearer before the key is written to it.
|
|
///
|
|
/// The values in this FST are not monotonically increasing when sorted
|
|
/// lexicographically by key, then this routine has unspecified behavior.
|
|
#[inline]
|
|
pub fn get_key_into(&self, value: u64, key: &mut Vec<u8>) -> bool {
|
|
self.as_ref().get_key_into(value, key)
|
|
}
|
|
|
|
/// Return a lexicographically ordered stream of all key-value pairs in
|
|
/// this fst.
|
|
#[inline]
|
|
pub fn stream(&self) -> Stream<'_> {
|
|
StreamBuilder::new(self.as_ref(), AlwaysMatch).into_stream()
|
|
}
|
|
|
|
/// Returns the number of keys in this fst.
|
|
#[inline]
|
|
pub fn len(&self) -> usize {
|
|
self.as_ref().len()
|
|
}
|
|
|
|
/// Returns true if and only if this fst has no keys.
|
|
#[inline]
|
|
pub fn is_empty(&self) -> bool {
|
|
self.as_ref().is_empty()
|
|
}
|
|
|
|
/// Returns the number of bytes used by this fst.
|
|
#[inline]
|
|
pub fn size(&self) -> usize {
|
|
self.as_ref().size()
|
|
}
|
|
|
|
/// Attempts to verify this FST by computing its checksum.
|
|
///
|
|
/// This will scan over all of the bytes in the underlying FST, so this
|
|
/// may be an expensive operation depending on the size of the FST.
|
|
///
|
|
/// This returns an error in two cases:
|
|
///
|
|
/// 1. When a checksum does not exist, which is the case for FSTs that were
|
|
/// produced by the `fst` crate before version `0.4`.
|
|
/// 2. When the checksum in the FST does not match the computed checksum
|
|
/// performed by this procedure.
|
|
#[inline]
|
|
pub fn verify(&self) -> Result<()> {
|
|
Ok(())
|
|
}
|
|
|
|
/// Returns the root node of this fst.
|
|
#[inline]
|
|
pub fn root(&self) -> Node<'_> {
|
|
self.as_ref().root()
|
|
}
|
|
|
|
/// Returns the node at the given address.
|
|
///
|
|
/// Node addresses can be obtained by reading transitions on `Node` values.
|
|
#[inline]
|
|
pub fn node(&self, addr: CompiledAddr) -> Node<'_> {
|
|
self.as_ref().node(addr)
|
|
}
|
|
|
|
/// Returns a copy of the binary contents of this FST.
|
|
#[inline]
|
|
pub fn to_vec(&self) -> Vec<u8> {
|
|
self.as_ref().to_vec()
|
|
}
|
|
|
|
/// Returns the binary contents of this FST.
|
|
#[inline]
|
|
pub fn as_bytes(&self) -> &[u8] {
|
|
self.as_ref().as_bytes()
|
|
}
|
|
|
|
#[inline]
|
|
fn as_ref(&self) -> FstRef {
|
|
FstRef { meta: &self.meta, data: self.data.as_ref() }
|
|
}
|
|
}
|
|
|
|
impl<D> Fst<D> {
|
|
/// Returns the underlying data which constitutes the FST itself.
|
|
#[inline]
|
|
pub fn into_inner(self) -> D {
|
|
self.data
|
|
}
|
|
|
|
/// Returns a borrow to the underlying data which constitutes the FST itself.
|
|
#[inline]
|
|
pub fn as_inner(&self) -> &D {
|
|
&self.data
|
|
}
|
|
|
|
/// Maps the underlying data of the fst to another data type.
|
|
#[inline]
|
|
pub fn map_data<F, T>(self, mut f: F) -> Result<Fst<T>>
|
|
where
|
|
F: FnMut(D) -> T,
|
|
T: AsRef<[u8]>,
|
|
{
|
|
Fst::new(f(self.into_inner()))
|
|
}
|
|
}
|
|
|
|
impl<'a, 'f, D: AsRef<[u8]>> IntoStreamer<'a> for &'f Fst<D> {
|
|
type Item = (&'a [u8], Output);
|
|
type Into = Stream<'f>;
|
|
|
|
#[inline]
|
|
fn into_stream(self) -> Stream<'f> {
|
|
StreamBuilder::new(self.as_ref(), AlwaysMatch).into_stream()
|
|
}
|
|
}
|
|
|
|
struct FstRef<'f> {
|
|
meta: &'f Meta,
|
|
data: &'f [u8],
|
|
}
|
|
|
|
impl<'f> FstRef<'f> {
|
|
#[inline]
|
|
fn get(&self, key: &[u8]) -> Option<Output> {
|
|
let mut node = self.root();
|
|
let mut out = Output::zero();
|
|
for &b in key {
|
|
node = match node.find_input(b) {
|
|
None => return None,
|
|
Some(i) => {
|
|
let t = node.transition(i);
|
|
out = out.cat(t.out);
|
|
self.node(t.addr)
|
|
}
|
|
}
|
|
}
|
|
if !node.is_final() {
|
|
None
|
|
} else {
|
|
Some(out.cat(node.final_output()))
|
|
}
|
|
}
|
|
|
|
#[inline]
|
|
fn contains_key(&self, key: &[u8]) -> bool {
|
|
let mut node = self.root();
|
|
for &b in key {
|
|
node = match node.find_input(b) {
|
|
None => return false,
|
|
Some(i) => self.node(node.transition_addr(i)),
|
|
}
|
|
}
|
|
node.is_final()
|
|
}
|
|
|
|
#[inline]
|
|
fn get_key_into(&self, mut value: u64, key: &mut Vec<u8>) -> bool {
|
|
let mut node = self.root();
|
|
while value != 0 || !node.is_final() {
|
|
let trans = node
|
|
.transitions()
|
|
.take_while(|t| t.out.value() <= value)
|
|
.last();
|
|
node = match trans {
|
|
None => return false,
|
|
Some(t) => {
|
|
value -= t.out.value();
|
|
key.push(t.inp);
|
|
self.node(t.addr)
|
|
}
|
|
};
|
|
}
|
|
true
|
|
}
|
|
|
|
#[inline]
|
|
fn len(&self) -> usize {
|
|
self.meta.len
|
|
}
|
|
|
|
#[inline]
|
|
fn is_empty(&self) -> bool {
|
|
self.meta.len == 0
|
|
}
|
|
|
|
#[inline]
|
|
fn size(&self) -> usize {
|
|
self.as_bytes().len()
|
|
}
|
|
|
|
#[inline]
|
|
fn root_addr(&self) -> CompiledAddr {
|
|
self.meta.root_addr
|
|
}
|
|
|
|
#[inline]
|
|
fn root(&self) -> Node<'f> {
|
|
self.node(self.root_addr())
|
|
}
|
|
|
|
#[inline]
|
|
fn node(&self, addr: CompiledAddr) -> Node<'f> {
|
|
Node::new(addr, self.as_bytes())
|
|
}
|
|
|
|
#[inline]
|
|
fn to_vec(&self) -> Vec<u8> {
|
|
self.as_bytes().to_vec()
|
|
}
|
|
|
|
#[inline]
|
|
fn as_bytes(&self) -> &'f [u8] {
|
|
self.data
|
|
}
|
|
|
|
#[inline]
|
|
fn empty_final_output(&self) -> Option<Output> {
|
|
let root = self.root();
|
|
if root.is_final() {
|
|
Some(root.final_output())
|
|
} else {
|
|
None
|
|
}
|
|
}
|
|
}
|
|
|
|
/// A builder for constructing range queries on streams.
|
|
///
|
|
/// Once all bounds are set, one should call `into_stream` to get a
|
|
/// `Stream`.
|
|
///
|
|
/// Bounds are not additive. That is, if `ge` is called twice on the same
|
|
/// builder, then the second setting wins.
|
|
///
|
|
/// The `A` type parameter corresponds to an optional automaton to filter
|
|
/// the stream. By default, no filtering is done.
|
|
///
|
|
/// The `'f` lifetime parameter refers to the lifetime of the underlying fst.
|
|
pub struct StreamBuilder<'f, A = AlwaysMatch> {
|
|
fst: FstRef<'f>,
|
|
aut: A,
|
|
min: Bound,
|
|
max: Bound,
|
|
}
|
|
|
|
impl<'f, A: Automaton> StreamBuilder<'f, A> {
|
|
fn new(fst: FstRef<'f>, aut: A) -> StreamBuilder<'f, A> {
|
|
StreamBuilder {
|
|
fst,
|
|
aut,
|
|
min: Bound::Unbounded,
|
|
max: Bound::Unbounded,
|
|
}
|
|
}
|
|
|
|
/// Specify a greater-than-or-equal-to bound.
|
|
pub fn ge<T: AsRef<[u8]>>(mut self, bound: T) -> StreamBuilder<'f, A> {
|
|
self.min = Bound::Included(bound.as_ref().to_owned());
|
|
self
|
|
}
|
|
|
|
/// Specify a greater-than bound.
|
|
pub fn gt<T: AsRef<[u8]>>(mut self, bound: T) -> StreamBuilder<'f, A> {
|
|
self.min = Bound::Excluded(bound.as_ref().to_owned());
|
|
self
|
|
}
|
|
|
|
/// Specify a less-than-or-equal-to bound.
|
|
pub fn le<T: AsRef<[u8]>>(mut self, bound: T) -> StreamBuilder<'f, A> {
|
|
self.max = Bound::Included(bound.as_ref().to_owned());
|
|
self
|
|
}
|
|
|
|
/// Specify a less-than bound.
|
|
pub fn lt<T: AsRef<[u8]>>(mut self, bound: T) -> StreamBuilder<'f, A> {
|
|
self.max = Bound::Excluded(bound.as_ref().to_owned());
|
|
self
|
|
}
|
|
}
|
|
|
|
impl<'a, 'f, A: Automaton> IntoStreamer<'a> for StreamBuilder<'f, A> {
|
|
type Item = (&'a [u8], Output);
|
|
type Into = Stream<'f, A>;
|
|
|
|
fn into_stream(self) -> Stream<'f, A> {
|
|
Stream::new(self.fst, self.aut, self.min, self.max)
|
|
}
|
|
}
|
|
|
|
#[derive(Debug)]
|
|
enum Bound {
|
|
Included(Vec<u8>),
|
|
Excluded(Vec<u8>),
|
|
Unbounded,
|
|
}
|
|
|
|
impl Bound {
|
|
#[inline]
|
|
fn exceeded_by(&self, inp: &[u8]) -> bool {
|
|
match *self {
|
|
Bound::Included(ref v) => inp > v,
|
|
Bound::Excluded(ref v) => inp >= v,
|
|
Bound::Unbounded => false,
|
|
}
|
|
}
|
|
|
|
#[inline]
|
|
fn is_empty(&self) -> bool {
|
|
match *self {
|
|
Bound::Included(ref v) => v.is_empty(),
|
|
Bound::Excluded(ref v) => v.is_empty(),
|
|
Bound::Unbounded => true,
|
|
}
|
|
}
|
|
|
|
#[inline]
|
|
fn is_inclusive(&self) -> bool {
|
|
!matches!(*self, Bound::Excluded(_))
|
|
}
|
|
}
|
|
|
|
/// A lexicographically ordered stream of key-value pairs from an fst.
|
|
///
|
|
/// The `A` type parameter corresponds to an optional automaton to filter
|
|
/// the stream. By default, no filtering is done.
|
|
///
|
|
/// The `'f` lifetime parameter refers to the lifetime of the underlying fst.
|
|
pub struct Stream<'f, A: Automaton = AlwaysMatch>(StreamWithState<'f, A>);
|
|
|
|
impl<'f, A: Automaton> Stream<'f, A> {
|
|
fn new(fst: FstRef<'f>, aut: A, min: Bound, max: Bound) -> Stream<'f, A> {
|
|
Stream(StreamWithState::new(fst, aut, min, max))
|
|
}
|
|
|
|
/// Convert this stream into a vector of byte strings and outputs.
|
|
///
|
|
/// Note that this creates a new allocation for every key in the stream.
|
|
pub fn into_byte_vec(mut self) -> Vec<(Vec<u8>, u64)> {
|
|
let mut vs = vec![];
|
|
while let Some((k, v)) = self.next() {
|
|
vs.push((k.to_vec(), v.value()));
|
|
}
|
|
vs
|
|
}
|
|
|
|
/// Convert this stream into a vector of Unicode strings and outputs.
|
|
///
|
|
/// If any key is not valid UTF-8, then iteration on the stream is stopped
|
|
/// and a UTF-8 decoding error is returned.
|
|
///
|
|
/// Note that this creates a new allocation for every key in the stream.
|
|
pub fn into_str_vec(mut self) -> Result<Vec<(String, u64)>> {
|
|
let mut vs = vec![];
|
|
while let Some((k, v)) = self.next() {
|
|
let k = String::from_utf8(k.to_vec()).map_err(Error::from)?;
|
|
vs.push((k, v.value()));
|
|
}
|
|
Ok(vs)
|
|
}
|
|
|
|
/// Convert this stream into a vector of byte strings.
|
|
///
|
|
/// Note that this creates a new allocation for every key in the stream.
|
|
pub fn into_byte_keys(mut self) -> Vec<Vec<u8>> {
|
|
let mut vs = vec![];
|
|
while let Some((k, _)) = self.next() {
|
|
vs.push(k.to_vec());
|
|
}
|
|
vs
|
|
}
|
|
|
|
/// Convert this stream into a vector of Unicode strings.
|
|
///
|
|
/// If any key is not valid UTF-8, then iteration on the stream is stopped
|
|
/// and a UTF-8 decoding error is returned.
|
|
///
|
|
/// Note that this creates a new allocation for every key in the stream.
|
|
pub fn into_str_keys(mut self) -> Result<Vec<String>> {
|
|
let mut vs = vec![];
|
|
while let Some((k, _)) = self.next() {
|
|
let k = String::from_utf8(k.to_vec()).map_err(Error::from)?;
|
|
vs.push(k);
|
|
}
|
|
Ok(vs)
|
|
}
|
|
|
|
/// Convert this stream into a vector of outputs.
|
|
pub fn into_values(mut self) -> Vec<u64> {
|
|
let mut vs = vec![];
|
|
while let Some((_, v)) = self.next() {
|
|
vs.push(v.value());
|
|
}
|
|
vs
|
|
}
|
|
}
|
|
|
|
impl<'f, 'a, A: Automaton> Streamer<'a> for Stream<'f, A> {
|
|
type Item = (&'a [u8], Output);
|
|
|
|
fn next(&'a mut self) -> Option<(&'a [u8], Output)> {
|
|
self.0.next_with(|_| ()).map(|(key, out, _)| (key, out))
|
|
}
|
|
}
|
|
|
|
/// A lexicographically ordered stream of key-value-state triples from an fst
|
|
/// and an automaton.
|
|
///
|
|
/// The key-values are from the underyling FSTP while the states are from the
|
|
/// automaton.
|
|
///
|
|
/// The `A` type parameter corresponds to an optional automaton to filter
|
|
/// the stream. By default, no filtering is done.
|
|
///
|
|
/// The `'m` lifetime parameter refers to the lifetime of the underlying map.
|
|
pub struct StreamWithState<'f, A = AlwaysMatch>
|
|
where
|
|
A: Automaton,
|
|
{
|
|
fst: FstRef<'f>,
|
|
aut: A,
|
|
inp: Vec<u8>,
|
|
empty_output: Option<Output>,
|
|
stack: Vec<StreamState<'f, A::State>>,
|
|
end_at: Bound,
|
|
}
|
|
|
|
#[derive(Clone, Debug)]
|
|
struct StreamState<'f, S> {
|
|
node: Node<'f>,
|
|
trans: usize,
|
|
out: Output,
|
|
aut_state: S,
|
|
}
|
|
|
|
impl<'f, A: Automaton> StreamWithState<'f, A> {
|
|
fn new(
|
|
fst: FstRef<'f>,
|
|
aut: A,
|
|
min: Bound,
|
|
max: Bound,
|
|
) -> StreamWithState<'f, A> {
|
|
let mut rdr = StreamWithState {
|
|
fst,
|
|
aut,
|
|
inp: Vec::with_capacity(16),
|
|
empty_output: None,
|
|
stack: vec![],
|
|
end_at: max,
|
|
};
|
|
rdr.seek_min(min);
|
|
rdr
|
|
}
|
|
|
|
/// Seeks the underlying stream such that the next key to be read is the
|
|
/// smallest key in the underlying fst that satisfies the given minimum
|
|
/// bound.
|
|
///
|
|
/// This theoretically should be straight-forward, but we need to make
|
|
/// sure our stack is correct, which includes accounting for automaton
|
|
/// states.
|
|
fn seek_min(&mut self, min: Bound) {
|
|
if min.is_empty() {
|
|
if min.is_inclusive() {
|
|
self.empty_output = self.fst.empty_final_output();
|
|
}
|
|
self.stack = vec![StreamState {
|
|
node: self.fst.root(),
|
|
trans: 0,
|
|
out: Output::zero(),
|
|
aut_state: self.aut.start(),
|
|
}];
|
|
return;
|
|
}
|
|
let (key, inclusive) = match min {
|
|
Bound::Excluded(ref min) => (min, false),
|
|
Bound::Included(ref min) => (min, true),
|
|
Bound::Unbounded => unreachable!(),
|
|
};
|
|
// At this point, we need to find the starting location of `min` in
|
|
// the FST. However, as we search, we need to maintain a stack of
|
|
// reader states so that the reader can pick up where we left off.
|
|
// N.B. We do not necessarily need to stop in a final state, unlike
|
|
// the one-off `find` method. For the example, the given bound might
|
|
// not actually exist in the FST.
|
|
let mut node = self.fst.root();
|
|
let mut out = Output::zero();
|
|
let mut aut_state = self.aut.start();
|
|
for &b in key {
|
|
match node.find_input(b) {
|
|
Some(i) => {
|
|
let t = node.transition(i);
|
|
let prev_state = aut_state;
|
|
aut_state = self.aut.accept(&prev_state, b);
|
|
self.inp.push(b);
|
|
self.stack.push(StreamState {
|
|
node,
|
|
trans: i + 1,
|
|
out,
|
|
aut_state: prev_state,
|
|
});
|
|
out = out.cat(t.out);
|
|
node = self.fst.node(t.addr);
|
|
}
|
|
None => {
|
|
// This is a little tricky. We're in this case if the
|
|
// given bound is not a prefix of any key in the FST.
|
|
// Since this is a minimum bound, we need to find the
|
|
// first transition in this node that proceeds the current
|
|
// input byte.
|
|
self.stack.push(StreamState {
|
|
node,
|
|
trans: node
|
|
.transitions()
|
|
.position(|t| t.inp > b)
|
|
.unwrap_or(node.len()),
|
|
out,
|
|
aut_state,
|
|
});
|
|
return;
|
|
}
|
|
}
|
|
}
|
|
if !self.stack.is_empty() {
|
|
let last = self.stack.len() - 1;
|
|
if inclusive {
|
|
self.stack[last].trans -= 1;
|
|
self.inp.pop();
|
|
} else {
|
|
let node = self.stack[last].node;
|
|
let trans = self.stack[last].trans;
|
|
self.stack.push(StreamState {
|
|
node: self.fst.node(node.transition(trans - 1).addr),
|
|
trans: 0,
|
|
out,
|
|
aut_state,
|
|
});
|
|
}
|
|
}
|
|
}
|
|
|
|
fn next_with<T>(
|
|
&mut self,
|
|
mut map: impl FnMut(&A::State) -> T,
|
|
) -> Option<(&[u8], Output, T)> {
|
|
if let Some(out) = self.empty_output.take() {
|
|
if self.end_at.exceeded_by(&[]) {
|
|
self.stack.clear();
|
|
return None;
|
|
}
|
|
|
|
let start = self.aut.start();
|
|
if self.aut.is_match(&start) {
|
|
return Some((&[], out, map(&start)));
|
|
}
|
|
}
|
|
while let Some(state) = self.stack.pop() {
|
|
if state.trans >= state.node.len()
|
|
|| !self.aut.can_match(&state.aut_state)
|
|
{
|
|
if state.node.addr() != self.fst.root_addr() {
|
|
self.inp.pop().unwrap();
|
|
}
|
|
continue;
|
|
}
|
|
let trans = state.node.transition(state.trans);
|
|
let out = state.out.cat(trans.out);
|
|
let next_state = self.aut.accept(&state.aut_state, trans.inp);
|
|
let t = map(&next_state);
|
|
let mut is_match = self.aut.is_match(&next_state);
|
|
let next_node = self.fst.node(trans.addr);
|
|
self.inp.push(trans.inp);
|
|
if next_node.is_final() {
|
|
if let Some(eof_state) = self.aut.accept_eof(&next_state) {
|
|
is_match = self.aut.is_match(&eof_state);
|
|
}
|
|
}
|
|
self.stack.push(StreamState { trans: state.trans + 1, ..state });
|
|
self.stack.push(StreamState {
|
|
node: next_node,
|
|
trans: 0,
|
|
out,
|
|
aut_state: next_state,
|
|
});
|
|
if self.end_at.exceeded_by(&self.inp) {
|
|
// We are done, forever.
|
|
self.stack.clear();
|
|
return None;
|
|
}
|
|
if next_node.is_final() && is_match {
|
|
return Some((
|
|
&self.inp,
|
|
out.cat(next_node.final_output()),
|
|
t,
|
|
));
|
|
}
|
|
}
|
|
None
|
|
}
|
|
}
|
|
|
|
impl<'a, 'f, A: 'a + Automaton> Streamer<'a> for StreamWithState<'f, A>
|
|
where
|
|
A::State: Clone,
|
|
{
|
|
type Item = (&'a [u8], Output, A::State);
|
|
|
|
fn next(&'a mut self) -> Option<(&'a [u8], Output, A::State)> {
|
|
self.next_with(|state| state.clone())
|
|
}
|
|
}
|
|
|
|
/// An output is a value that is associated with a key in a finite state
|
|
/// transducer.
|
|
///
|
|
/// Note that outputs must satisfy an algebra. Namely, it must have an additive
|
|
/// identity and the following binary operations defined: `prefix`,
|
|
/// `concatenation` and `subtraction`. `prefix` and `concatenation` are
|
|
/// commutative while `subtraction` is not. `subtraction` is only defined on
|
|
/// pairs of operands where the first operand is greater than or equal to the
|
|
/// second operand.
|
|
///
|
|
/// Currently, output values must be `u64`. However, in theory, an output value
|
|
/// can be anything that satisfies the above algebra. Future versions of this
|
|
/// crate may make outputs generic on this algebra.
|
|
#[derive(Copy, Clone, Debug, Hash, Eq, Ord, PartialEq, PartialOrd)]
|
|
pub struct Output(u64);
|
|
|
|
impl Output {
|
|
/// Create a new output from a `u64`.
|
|
#[inline]
|
|
pub fn new(v: u64) -> Output {
|
|
Output(v)
|
|
}
|
|
|
|
/// Create a zero output.
|
|
#[inline]
|
|
pub fn zero() -> Output {
|
|
Output(0)
|
|
}
|
|
|
|
/// Retrieve the value inside this output.
|
|
#[inline]
|
|
pub fn value(self) -> u64 {
|
|
self.0
|
|
}
|
|
|
|
/// Returns true if this is a zero output.
|
|
#[inline]
|
|
pub fn is_zero(self) -> bool {
|
|
self.0 == 0
|
|
}
|
|
|
|
/// Returns the prefix of this output and `o`.
|
|
#[inline]
|
|
pub fn prefix(self, o: Output) -> Output {
|
|
Output(cmp::min(self.0, o.0))
|
|
}
|
|
|
|
/// Returns the concatenation of this output and `o`.
|
|
#[inline]
|
|
pub fn cat(self, o: Output) -> Output {
|
|
Output(self.0 + o.0)
|
|
}
|
|
|
|
/// Returns the subtraction of `o` from this output.
|
|
///
|
|
/// This function panics if `self < o`.
|
|
#[allow(clippy::should_implement_trait)]
|
|
#[inline]
|
|
pub fn sub(self, o: Output) -> Output {
|
|
Output(
|
|
self.0
|
|
.checked_sub(o.0)
|
|
.expect("BUG: underflow subtraction not allowed"),
|
|
)
|
|
}
|
|
}
|
|
|
|
/// A transition from one note to another.
|
|
#[derive(Copy, Clone, Hash, Eq, PartialEq)]
|
|
pub struct Transition {
|
|
/// The byte input associated with this transition.
|
|
pub inp: u8,
|
|
/// The output associated with this transition.
|
|
pub out: Output,
|
|
/// The address of the node that this transition points to.
|
|
pub addr: CompiledAddr,
|
|
}
|
|
|
|
impl Default for Transition {
|
|
#[inline]
|
|
fn default() -> Transition {
|
|
Transition { inp: 0, out: Output::zero(), addr: NONE_ADDRESS }
|
|
}
|
|
}
|
|
|
|
impl fmt::Debug for Transition {
|
|
fn fmt(&self, f: &mut fmt::Formatter<'_>) -> fmt::Result {
|
|
if self.out.is_zero() {
|
|
write!(f, "{} -> {}", self.inp as char, self.addr)
|
|
} else {
|
|
write!(
|
|
f,
|
|
"({}, {}) -> {}",
|
|
self.inp as char,
|
|
self.out.value(),
|
|
self.addr
|
|
)
|
|
}
|
|
}
|
|
}
|
|
|
|
#[inline]
|
|
#[cfg(target_pointer_width = "64")]
|
|
const fn u64_to_usize(n: u64) -> usize {
|
|
n as usize
|
|
}
|
|
|
|
#[inline]
|
|
#[cfg(not(target_pointer_width = "64"))]
|
|
const fn u64_to_usize(n: u64) -> usize {
|
|
if n > std::usize::MAX as u64 {
|
|
panic!(
|
|
"\
|
|
Cannot convert node address {} to a pointer sized variable. If this FST
|
|
is very large and was generated on a system with a larger pointer size
|
|
than this system, then it is not possible to read this FST on this
|
|
system.",
|
|
n
|
|
);
|
|
}
|
|
n as usize
|
|
}
|